Introduction
How can symbolic artificial intelligence be used to create expert systems? Typically, symbolic or logical AI deal with using knowledge-bases and rule-sets in order to make intelligent decisions. These types of expert systems can provide powerful results and are used in many real-world applications from healthcare to taxes.
Machine learning has become one of the most common artificial intelligence topics discussed in both the business world and the media today. However, many different areas of artificial intelligence exist beyond machine learning. One of those areas includes the topic of symbolic (or logic-based) artificial intelligence, also called classical AI.
Symbolic AI had one of its biggest successes with Shakey the Robot, a ground-breaking project by Stanford Research Institute in 1972. It was the first robot that could perceive and reason about its world and surroundings. The means from which it could reason resided within hard-coded and human-designed rules that provided the knowledge-base from which the robot would base its actions. In fact, the project was the originator of the A* search algorithm, as well as the Stanford Research Institute Problem Solver (or STRIPS) automated planner.
Symbolic Artificial Intelligence
Symbolic artificial intelligence was the most common type of AI implementation through the 1980’s. Rule-based engines and expert systems dominated the application space for AI implementations. One of the longest running implementations of classical AI is the Cyc database project. It uses a massive ontology of rules and facts with the goal of capturing human common sense. It was reasoned that a large enough knowledge-base could potentially lead to strong-AI. The Cyc project could even be thought of as the predecessor to IBM Watson, which itself, includes a massive knowledge-base of domain-specific rules, facts, and conclusions. IBM Watson can also be considered an expert system, although it also includes machine learning technologies, for example for natural language processing.
Modern day applications of symbolic AI exist within expert systems such as tax processing software, customer service and technical support systems, medical diagnosis systems, and even many natural language platforms, including Amazon Alexa apps, utilize methods in symbolic artificial intelligence. In the case of chat bots, this can include sets of rules, based upon specific keywords and conversation state, to execute varying responses to queries.
In this tutorial, we’re going to walk through some of the background behind logical artificial intelligence by reviewing propositional logic and first-order logic. We’ll then walk through the steps of creating our own knowledge-base and associated expert system for selecting financial ETF funds based upon preferences from the user. We’ll represent our knowledge using Javascript and JSON and query against the knowledge-base with forward chaining and backward chaining logic-based artificial intelligence algorithms.
Let’s start by taking a look at some of the methods used within logical artificial intelligence.
Developing Logical Rules for Symbolic AI
Symbolic artificial intelligence uses human-readable logical representations of knowledge in order to provide intelligent decisions. This is in contrast to machine learning, which uses supervised and unsupervised learning with large training sets to determine statistically important properties of the data and generalize about the results. Symbolic AI does not employ training in this manner, and rather utilizes predetermined rules and facts about its world and environment.
Rules for logical-based AI can be provided in the form of propositional logic, as shown below.
1 | Today it is snowing. |
The above statements can be represented in propositional logic as follows.
1 | P: Today it is snowing. |
The statement “If today it is snowing, then today is cold” is represented by the propositional function P => Q. We can prove propositional statements with truth tables, providing for a precise logical conclusion for arguments programmed into a symbolic AI system.
P | Q | P =>Q
- T T T
- T F F
- F T T
- F F T
The above truth tables shows that in every world in which P and P => Q are true (row 1), Q is also true, showing that the premises support the conclusion with a sound argument. That is, in all cases where it’s snowing today and “if today it is snowing, then today is cold” are true then it is also true that today is cold,. This makes sense if you consider the argument.
Consider the alternative cases from the truth table.
Row 2. If it is snowing today, but today is not cold, then the statement “If today it is snowing, then today is cold” is not true - since it is somehow snowing today even though it’s not cold!
Row 3. Likewise, the next row implies that it is not snowing today, but it is cold, therefore the statement “if today it is snowing, then today is cold” still holds true, because even though it’s cold today yet not snowing doesn’t negate the statement that when it does snow, it’s cold.
Row 4. The final row states if it is not snowing and it’s not cold (for example, a summer day). The conclusion is still true that if it’s snowing today then it’s cold, since a summer day doesn’t refute this conclusion. All of these statements make sense and are, thus, valid arguments.
Upgrading to First-Order Logic
Propositional logic can be implemented within an expert system using symbolic AI. However, in order to make it easier for humans to write this form of logic, in a means easily understood by computers, we can utilize first-order logic.
An example of first-order logic is shown below.
1 | weather(snow) |
The above is a form of first-order logic) that can be implemented in the Prolog programming language. A simple example is shown below.
1 | weather(cold) :- weather(snow). |
As you can see in the above example, we’ve included a rule for if the weather is snow, then the weather is also cold. We’ve also provided a fact to the knowledge-base that the weather is currently snow. When we then query for what the weather is, the program responds with the weather being cold and snow. Just as we’ve proven with propositional logic, the program written using first-order logic also runs in the same fashion.
1 | weather(warm). |
As a counter-example, we can change our single fact to weather(warm) and run the program again. This time, the output is simply weather(warm) and does not include snow, as expected.
You can create more expressive logical propositional statements by using operators such as AND, OR, NOT, IF, IF AND ONLY IF, as well as quantifiers such as FOR ALL and THERE EXISTS.
For example. We previously stated that if today it is snowing, then today it is cold, shown by the propositional statements below.
1 | P: Today it is snowing. |
We could also state the following expression.
1 | forall(x) snowing(x) => iscold(x) |
The above statement describes that for all days (x) where it is snowing, it is also cold.
Taxonomies
We can further express logical statements along with properties of entities and their relationships to other entities. In this manner, we can provide an artificial intelligence system with knowledge about a concept, its properties, and related concepts. By forming a hierarchy of concepts we can create an ontology knowledge-base that can encompass a large variety of concepts about a given subject or domain.
For example, in the above domain of it snowing and being cold, we might express the entity of snow as being related to the entity of ice. It can also be related to water, as well as to having properties for temperature. For example, we might show the following relationships.
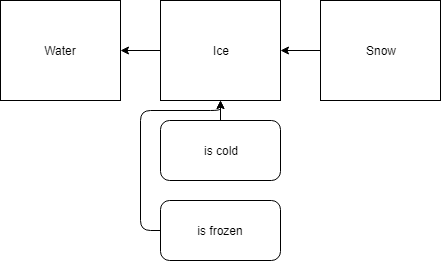
1 | forall(x) snow(x) => ice(x) |
In the above taxonomy, we’ve declared snow to be a subset of ice, and ice to be a subset of water. Since ice has the properties of being cold and frozen, all entities that are a subset of it also inherit the properties of being cold and frozen. Thus, snow is also cold and frozen.
Exceptions to the Rule
Now, there could be situations where snow is not cold. An example of this might be a movie set where artificial snow is being used and the snow is made of paper or confetti. In this case, the studio could be warm and yet it is snowing, which invalidates our taxonomy of logical relationships. An artificial intelligence built using the original logic would fail to make the appropriate deduction in this situation, since it is not aware of artificial snow or of the possibility of snow not being cold.
Circumscription can be used to resolve this type of abnormality, by assuming that everything is as expected, unless stated otherwise. That is, the propositional statement holds true for all cases (even exceptional or abnormal ones) unless it is explicitly stated that the condition is abnormal and should be considered.
Using circumscription, we could better express our original statement as follows.
1 | forall(x) ice(x) ^ !abnormal(x) => iscold(x) |
The above statement describes that for all types of ice where it is not abnormal, it is also cold. Recall that since snow is a subset of ice, it also inherits the same properties. In the case of the movie studio with artificial snow or a rare weather condition creating snow on a spring day, we could express those situations with the following statement.
1 | forall(x) artificialsnow(x) => snow(x) |
With the above explicitly expressed abnormality, “artificialsnow” is a subset of snow. Since we’ve defined “artificialsnow” to also be abnormal, our newly formatted circumscription statement will hold true. In this case, “artificialsnow”, will not inherit the “iscold” property.
We can demonstrate circumscription in the following Prolog program.
1 | snow(X) :- artificialsnow(X). |
Notice, the above program declares our taxonomy of “artificialsnow” as being a subset of “snow”. We further define “snow” to be a subset as “ice”. We then define the properties “isfrozen” and “iscold” to exist for entities of type “ice”. Finally, we define the entity“flake” as being of type “snow”, and “confetti” as being of type “artificialsnow”. Since “artificialsnow” inherits from snow, and snow inherits from ice, they both receive the “isfrozen” and “iscold” properties.
If we run and query the above program, we can see the following output.
1 | ?- iscold(flake) |
Now, since confetti is artificial snow, it deserves to be treated as an exceptional case. It should not contain the “iscold” property, which it inherits from snow (and thus, from ice). We can use circumscription to define this exception by changing our program as shown below.
1 | snow(X) :- artificialsnow(X). |
We’ve modified the original rule for iscold(X) to now specify not(abnormal(X)). We further define abnormal(X) to pertain to “artificialsnow”. With these rules in place, we can now query the knowledge-base again and obtain the correct response that “confetti” is not cold.
1 | ?- iscold(flake) |
Expert Systems
Common examples of systems that utilize symbolic AI include knowledge-base databases and expert systems. Since the knowledge provided to the system is typically provided by a human expert, the systems are usually designed specifically for a target domain or industry.
Human Defined Knowledge Base
An expert system contains its knowledge usually in the form of a database or knowledge-base. By decoupling the knowledge from the actual software algorithm, an expert system can navigate through the database of facts to determine classifications and make decisions. The database is typically created by a human expert, and as such, the extent of knowledge that an expert system contains is typically confined to that of the human providing the content.
For example, a medical diagnosis expert system may contain a knowledge-base consisting of many different facts about diseases, symptoms, and conditions. The data can usually be represented by a tree hierarchy, from which one could navigate through the branches of symptoms until a particular conclusion is reached (i.e., a specific disease or condition). By using a logic-based AI algorithm on the knowledge-base, such as forward-chaining and backward-chaining, an algorithm can intelligently traverse the tree, narrowing down the conclusion based upon the patient’s provided symptoms.
Designing Your Own Expert System
Now that we’ve covered an overview of the background behind logical-based artificial intelligence, let’s take a look at how you can create your own expert system with symbolic AI.
We’ll design a simple knowledge-base for selecting financial ETF funds according to preferences from the user, using Javascript and JSON. The first task is to determine a schema for our knowledge-base to represent the rules.
Knowledge Representation
Symbolic AI offers several methods for traditional representation of knowledge. Specifically, a format is required that contains premises and conclusions. Each premise will contain preconditions that much be satisfied in order for the conclusion to be valid. When a conclusion is deemed valid, it’s attribute will be added to the current list of assertions from the original query.
Expert systems using symbolic AI typically work by maintaining an active list of assertions for the current query and comparing those against the rules within the knowledge-base. When a rule’s preconditions are all held to be true, compared to the current set of assertions, that rule triggers. That is, when all preconditions of a rule exist within the current list of assertion attributes, the rule executes.
As an example, suppose the user is querying an expert system about health. The user wants to know if they’re sick. We have the following rules defined in our knowledge-base.
1 | IF fever is yes |
Our program begins with an empty set of assertions. The assertion set in memory appears as follows.
1 | assertions = () |
The user provide their symptoms to the program, as shown below.
1 | fever = no |
Our program’s assertion set in memory now appears as follows.
1 | assertions = fever(no), cough(yes), runnynose(yes) |
The symptoms provided by the user are added as assertions to our set of attributes within our program. We can then search against our knowledge base to check if any of the rules trigger. In this case, the first rule fails to trigger, as it requires fever to have the value of yes, but the user did not provide this value. Next, the second rule is examined. This one does, indeed, fire as all three conditions are held true from the user’s input. Thus, we add the conclusion diagnosis with the value cold to our current set of assertions.
The list of assertions in memory now shows as follows.
1 | assertions = fever(no), cough(yes), runnynose(yes), diagnosis(cold) |
Deducing Conclusions from a Knowledge-Base
A knowledge base becomes more powerful when we can enact intelligent behavior to deduce additional facts, beyond what the user had originally entered. Forward-chaining is one method of doing this.
As an example, suppose we extend our knowledge-base to include additional rules as follows.
1 | IF diagnosis is infection |
Recall that when our program ran with the initial user provided symptoms, we added the assertion diagnosis to our list of assertions in memory. When this change occurs, we can scan the knowledge-base again to check for any additionally satisfied rules and add those, as well, to the current assertion list.
In the above case, the second new rule will fire since diagnosis has the value cold. Thus, we will add its conclusion of medicine and the value acetaminophen to our assertion list.
1 | assertions = fever(no), cough(yes), runnynose(yes), diagnosis(cold), medicine(acetaminophen) |
With this result, our program could display to the user the diagnosis and the treatment.
Creating a Knowledge-Base in Javascript
In this project, we’re going to create a knowledge-base for ETF funds, corresponding to varying characteristics of each fund. We’ll need to include properties such as the fund name, type, category, as well as other properties specific to each. A brief overview of the design for our knowledge-base can be seen below.
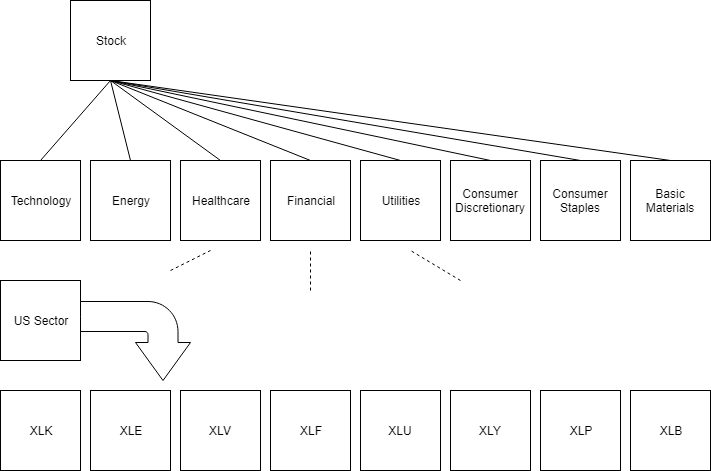
We can use the JSON format to implement the design for our knowledge-base. This will allow for an easily readable format for Javascript and node.js We’ll start by defining a schema for our rules to consist of premises and conclusions. An example for two ETF funds is shown below.
1 | const KB = [ |
The first rule shown above states that the preconditions are that the type must contain the value of bond, the category must contain the value of medium and the sector must contain the value of broad. If all three of these premises are valid, then the rule triggers and the conclusion fund with the value BND is added to the current set of assertions.
You can view a complete example of the ETF funds dataset to see the full knowledge-base.
With our knowledge-base defined, we can now begin querying against it using the techniques of forward-chaining and backward-chaining to deduce conclusions.
Forward Chaining
Querying a knowledge-base can be similar to following a set of if-then conditional statements, as we’ve demonstrated above. However, we can intelligently traverse the knowledge through the usage of techniques such as forward-chaining and backward-chaining, in order to deduce as much knowledge as possible from the original user input.
Forward chaining is the process of traversing through the knowledge-base from top to bottom, seeking a rule by which all attributes are satisfied. For example, if every single one of a rule’s attributes exist within the set of the user’s input, then that rule triggers, thus providing a conclusion. If no rule is found with all of the attributes present from the user, then no conclusions are added.
Forward chaining is an inference engine that works by having the user provide as much input, upfront, as they currently know. This includes specifying attributes and their values (assertions) before-hand and then performing a search against the database. Forward-chaining then cycles through all rules in the knowledge-base, comparing the current set of assertions (this includes those initially provided by the user, as well as additional ones deduced) against the premises of each rule. When a rule is satisfied by having all of its premises as true, its conclusion is added to the user’s assertion set and the set of rules is traversed again. Since a conclusion of one rule may be a prerequisite in another, we go back to the first rule and check for satisfied rules again.
This process can be optimized to prevent having to go back to the beginning of the rule set each time a new conclusion is added to the assertion list. This can be done by prioritizing the rules based upon their premises, so that rules that require prior rules’ conclusions are found after the parent rule (i.e., in ascending order).
The Forward Chaining Algorithm
The algorithm for performing forward chaining against a knowledge-base consists of traversing the set of rules. We can do this with a simple loop which checks each rule’s preconditions. When a rule triggers due to all of its preconditions being satisfied, and we have not yet added this rule to our list, we add the rule’s conclusion to the assertion list, reset the while loop back to the beginning, and iterate from the start.
The complete forward chaining algorithm in JavaScript can be found below.
1 | const forwardChain = function(assertions) { |
The key piece to the above code is the main while loop and the check for all premises being true with the current rule. This indicates that a rule will trigger. If it does, we make sure it’s not a duplicate, and then add it to the list of assertions. The final important piece for deducing additional assertions beyond the initial user input, is resetting ruleIndex back to zero. This starts the loop back at the first rule so that it can potentially trigger additional rules, based upon the newly updated list of assertions.
Let’s take a closer look at how a rule triggering can cause another rule to trigger.
Intelligent Deduction in Forward Chaining
As we’ve seen above in the forward chaining algorithm, when a rule triggers, its conclusion is added to our current list of assertions. This extends the input originally entered by the user. Since we now have additional assertions, new rules might trigger which require the new assertion as a premise.
Consider the following example. We have a particular ETF fund SDY that has the premises type, dividend, quality, and high yield. Let’s suppose that the user does not provide the dividend attribute. When the rule first runs, it will not trigger, as it is missing the dividend attribute from the list of current assertions. However, we have an additional rule in our knowledge-base that triggers from the attribute high yield having the value of yes. When this rule triggers, it adds the attribute dividend to the current list of assertions. This makes sense, since a user looking for high yield financial funds is also looking for dividend funds. When the loop runs a second time against the rules, the “high yield” rule will be skipped, since we’ve already triggered it, but the “SDY” rule will now trigger since all of its premises are satisfied.
1 | { |
Output
Here is an example of running the program using the above described input.
1 | Enter an attribute? type |
1 | [ { attribute: 'type', value: 'stock' }, |
Notice how the user inputs 3 attributes (assertions). After running the forward-chaining algorithm, we add an additional 2 attributes to the list, including the selected ETF fund, SDY.
Backward Chaining
In contrast to forward-chaining, backward-chaining tries to first locate a rule who’s conclusion matches one of the user’s provided attributes. When a rule is found, the process repeats, using the discovered rule’s attributes as new goals. The user is prompted to enter new values for attributes as they are discovered through the process. Once the algorithm satisfies all attributes for the chain of rules it can return the response to the user’s original query.
The Backward Chaining Algorithm
The algorithm for performing backward chaining against the knowledge-base is shown below. The key part of the algorithm is the parent loop, which iterates across the knowledge-base rule set. Additionally, an inner while loop iterates across each premise within the rule. This is required since, for each premise, we may need to recurse backwards to satisfy the premises for each parent premise. In doing so, we can query the user for additional attribute values, and upon satisfying parent premises, add new assertions to our list, hopefully triggering the final child rule.
The method begins by first checking if the current goal assertion exists within the current list of assertions. Initially, the only assertion in the list will be the user’s original goal. If the assertion does not exist, we’ll begin looping through the rule set. Each rule contains a list of premises that must be satisfied in order for a rule to trigger. We use recursion to call the backChain algorithm again on each premise, further querying for attributes, until the premise is satisfied or skipped, thus satisfying the rule or skipping the rule and moving on to the next.
When an assertion from a rule can not be determined, we query the user to provide a value for the attribute. If a value is provided, we can check if the premise is satisfied or branch to a different one. Likewise, if no value is provided, we know that this premise (and thus, the rule) does not apply to the user’s initial goal.
In this manner, we can intelligently traverse the knowledge-base as we narrow down on a target rule to satisfy the user’s query.
The backchaining algorithm is shown below.
1 | const backChain = function(goal, assertions) { |
Output
Below is an example of running the back chaining algorithm against the knowledge-base.
1 | What attribute type do you want to know? fund |
In the above example, the user wants to know the name of an ETF fund based upon their preferences. They begin by entering the attribute name fund. After providing this input, the back chaining algorithm begins. It starts with the first rule that contains the goal attribute (fund) within its conclusion - which happens to be for RWO.
1 | { |
The algorithm sees the first premise relating to type. Since no assertion for type exists within the current set of assertions, the program back-chains, trying to find a rule containing a conclusion of type. Since no rule exists that contains a conclusion of type, the algorithm asks the user to provide a value. The user enters stock.
With the first premise satisfied with type=stock, the algorithm now continues to the second premise, which is to satisfy category. Since no other rule contains a conclusion with the value category, the user is prompted to provide a value. The user chooses to skip this attribute, and so, the premise is not satisfied, and the current rule for RWO does not trigger.
The algorithm resumes traversing the rule set to satisfy the current list of assertions, skipping all rules that contain a category premise, arriving at the rule for PID.
1 | { |
The first premise type is already satisfied from the previous step, using the value stock. The next premise that is not yet satisfied is for the attribute dividend. Thus, the algorithm sets a new child goal of obtaining a value for dividend, recursing through the rule-set, until it locates a rule with a conclusion for dividend. It finds one, containing a single premise for high yield. Since no other rule contains a conclusion for high yield, the user is prompted to enter a value. In the case, the user enters yes.
Notice this key part of the backchain process. Rather than asking the user for the value of dividend directly, it instead follows the premises from a rule that contains dividend as its conclusion, and thus asks the user about the first premise for this rule, which is high yield. If the user can provide a value for this premise (and any other premises that this rule requires), the rule can be satisfied, and the premise for dividend can subsequently be satisfied.
With this new attribute, the recursion process returns back to the parent rule (for PID), satisfies the dividend attribute, and now tries to satisfy the next attribute for quality. Since no other rule contains quality as a conclusion, the user is prompted for a value.
After entering a value, the next premise for high yield was already satisfied through the back chaining recursive process, so we skip to satisfying international. Once again, since no rule exists with international as its conclusion, the user is prompted for a value, which they leave as blank. Therefore, this rule fails to trigger and we resume iterating to the next rule.
The subsequent rules requiring category or differing values for high yield and quality are skipped, since they don’t match the user’s current set of assertions. The first rule that matches the assertion list is SDY.
1 | { |
Since this rule has all of its premises satisfied, there is no need to back-chain and recurse to satisfy any of its premises. In this case, we simply add its conclusion to the assertion set and, since the conclusion is fund, it matches the user’s original goal. Thus, we terminate the back chain process and return the result as the output from the program.
Download @ GitHub
The source code for this project is available on GitHub.
About the Author
This article was written by Kory Becker, software developer and architect, skilled in a range of technologies, including web application development, artificial intelligence, machine learning, and data science.
Sponsor Me